はじめに
BIP32 に従ってあるシードから派生させた鍵があるとき、たとえばそれが non-hardened なノードだった場合に、元のシードの情報をどれくらい知りえるでしょうか?
ここでは以下を仮定して、シードの秘密鍵を得ることができないか検討してみます。
- シードの xpub を知っている
- ノード
m/0の秘密鍵を知っている
BIP32 を見てみる
BIP32 によると、 秘密鍵は以下のように作られるとされています。
- Check whether i ≥ 231 (whether the child is a hardened key).
- If so (hardened child): let I = HMAC-SHA512(Key = cpar, Data = 0x00 || ser256(kpar) || ser32(i)). (Note: The 0x00 pads the private key to make it 33 bytes long.)
- If not (normal child): let I = HMAC-SHA512(Key = cpar, Data = serP(point(kpar)) || ser32(i)).
- Split I into two 32-byte sequences, IL and IR.
- The returned child key ki is parse256(IL) + kpar (mod n).
最後の
ki is parse256(IL) + kpar (mod n)
に注目してみましょう。ここで parse256 はバイト列を256ビット整数に変換する関数、 n は楕円曲線のオーダー1 です。 lL の元になっている l ですが non-hardened の場合
I = HMAC-SHA512(Key = cpar, Data = serP(point(kpar)) || ser32(i))
であるとされています。ここでserP は公開鍵のシリアライズ、 ser32 は256ビット整数のシリアライズを表しています。 cpar はシード xpub の chain-code 、 kpar は公開鍵です。 i はノードのインデックス (m/0 の 0 の部分) で、これらは仮定から既知です。つまり、 lL は既知の情報で計算が可能ということになります。
parse256(lL) を L とおくと、秘密鍵の導出は
k_i = L + k_{par} \mod n\ ...\ (式1)となります。
仮定から ki は既知ですから、式1を満たす kpar を見つければシードの秘密鍵がわかるということになります。
やってみた
require 'bitcoin'
idx = 0
# ランダムにシードを作る
xprv = Bitcoin::ExtKey.generate_master(rand(1<<256).to_s(16))
puts "ppriv: #{xprv.priv}"
# 秘密鍵、xpubを生成
priv = xprv.derive(idx, false).priv
xpub = xprv.ext_pubkey
puts "xpub: #{xpub.to_base58}"
puts "priv: #{priv}"
data = xpub.pub.htb << [idx].pack('N')
l = Bitcoin.hmac_sha512(xpub.chain_code, data)
left = l[0..31].bth.to_i(16)
# privから逆算
pp = priv.to_i(16) - left
if pp < 0
pp += Bitcoin::CURVE_ORDER
end
ppriv = pp.to_s(16)
puts "ppriv: #{ppriv}"式1は加法のみからなる式なので、 kpar を求めるには引き算をすればよさそうです。ただし、 (mod n) をしているため、答えが 0 ~ (n-1) の範囲でなければ n を足すという処理をしています。3
実際に実行すると
$ ruby main.rb
ppriv: b1c7055860d84de5e34e031e309864948f842d451133acf3ac16a7624b09bb4a
xpub: xpub661MyMwAqRbcFi1XViMXFQM3RyASbwHg58RxiTLEB7EhnmuUdtQpcoMviDsdg3LcmWMhk4218kyFzzxdsSEifVgW42peizDd4QLEcVXn2Pr
priv: bd1a7de876cb012a1b554cbd5717e885761dcf931d017d859451c971a4dd031b
ppriv: b1c7055860d84de5e34e031e309864948f842d451133acf3ac16a7624b09bb4aという具合に、シードの秘密鍵が逆算できました✌️
まとめ
ある仮定のもとに、 non-hardened なノードからシードの秘密鍵が逆算できることがわかりました。つまり、そのシード下のすべての秘密鍵が計算できることになります。
鍵の管理には十分気をつけましょう!
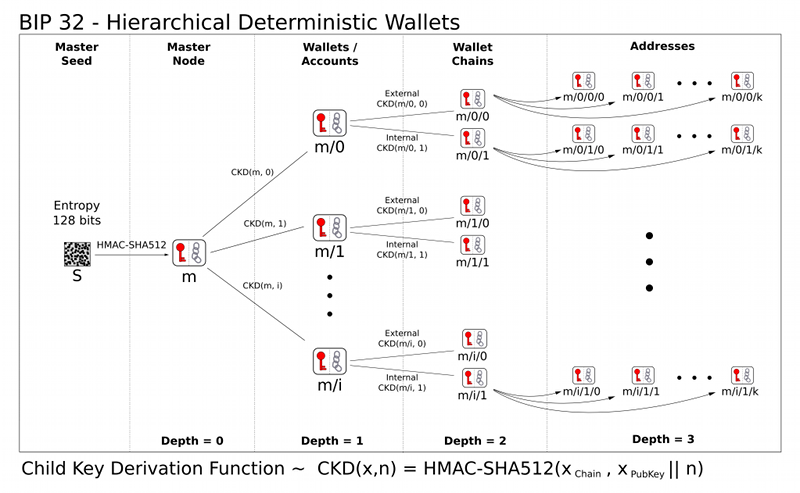
※ アイキャッチ画像は BIP32 の図より